Table of Contents
Introduction
A quadtree is a tree where each node has exactly four children. One application is storing 2D data by recursively dividing larger squares into four quadrants (top-left, top-right, bottom-left, bottom-right) and storing these in the tree. Once some condition is fulfilled, e.g. all the pixels in the square have a similar color, the process stops and the square is stored as a leaf.
While experimenting with operations on images compressed this way, a bug in my code produced this image:

As a reference, the original images looks like this:

Why is there a Sierpinsky Triangle hidden in there?
After a bit of debugging, I found out that the upper right corner of each node was not drawn.
The broken images nicely shows how the images is "compressed" by storing parts with the same color as larger squares.
In the upper left, a piece of sky is stored as a big square whereas on the container below the sierpinsky triangles are very visible because the cells of the quadtree are so small.
What other kinds of patterns and fractals can be generated this way?
Patterns
A pattern is a list of four "pattern elements", one for each quadrant of the quadtree. These element can either be constant colors or references to other patterns.
This forms a subset of the context-free grammars (Chomsky Type-2), the ones with exactly four terminals and non-terminals on the right-hand-side.
In addition to that, each reference to other patterns needs a fallback color to be used once the cells are to small to be divided further.
Systems With One Rule
Ignoring rotations and different colors, there are only a handful of systems with a single rule.
S -> white green blue S | white

S -> S red green S | red

S -> red S yellow S | yellow

S -> S blue S S | white

There is the Sierpinski Triangle again.
Systems With Two Rules
Adding more rules, the number of possible grammars quickly grows.
S -> T red green T | red T -> blue S S yellow | blue

Small changes to the rules lead to very different images.
S -> red T green T | red T -> S blue S yellow | blue

S -> red T T green | red T -> yellow S S blue | blue

S -> brown T T T | brown T -> yellow S S S | yellow

Chance and Necessity
These rule systems are already pretty powerful but I'd like to have a bit more variation.
An easy way to do this is allowing multiple rules
with the same left-hand-side (the part before the
->
)
and randomly choosing one on each iteration.
S -> blue S S yellow | yellow S -> S red green S | red

S -> S S S white | white S -> S S S blue | blue S -> S S S green | green S -> S S S red | red S -> S S S yellow | yellow

Now the
RuleSet
contains a list of patters for each index
and each time one is chosen at random.
impl Index<usize> for RuleSet { type Output = Pattern; fn index(&self, i: usize) -> &Pattern { let mut rng = self.rng.borrow_mut(); let j = rng.gen_range(0, self.rules[i].len()); &self.rules[i][j] } }
S -> S S S yellow | yellow S -> S blue S S | blue S -> white S S red | red

Letting the Computer do the Work
At this point, the hardest part is finding sets of rules that produce interesting images. Luckily, that's easy to automate by generating random rule sets and choosing the ones that look the best.
When generating a branch of rule, the probability a reference to another rule is chosen is 75%, otherwise a constant color is used.
For rules with at least one constant color, the last of them is used as fallback color, otherwise a random one is generated.
Due to the way the systems are generated,
there is a chance some of the rules can't be reached from the starting symbol (
S
in the previous sections,
0
for the randomly generated ones).
Here are a few of my favorites with different color pallets and parameters.
Black & White, 2 to 4 rules with 1 branch
0 -> 1 2 2 0 | black 1 -> black 1 1 black | black 2 -> white 2 2 black | black 3 -> 3 1 white 2 | white

0 -> white 1 0 0 | white 1 -> 1 black 1 white | white

0 -> 1 black 0 1 | black 1 -> 0 1 white 1 | white

0 -> 1 0 black 1 | black 1 -> 1 0 white 1 | white

0 -> black 0 2 black | black 1 -> 2 0 white 2 | white 2 -> 0 1 3 2 | black 3 -> 3 1 white 2 | white

0 -> 2 0 2 1 | white 1 -> black 2 2 1 | black 2 -> 2 0 0 1 | black

base16 colors + white, 2 to 4 rules with 1 branch
0 -> yellow 0 1 red | red 1 -> white 1 1 cyan | cyan

0 -> 1 2 3 2 | green 1 -> red 3 0 purple | purple 2 -> 3 yellow 3 0 | yellow 3 -> red white brown brown | brown

0 -> 1 blue 1 0 | blue 1 -> 0 white 0 green | green

0 -> 1 white blue 1 | blue 1 -> 0 brown 0 0 | brown 2 -> 0 2 yellow 1 | yellow

0 -> 0 0 1 0 | yellow 1 -> yellow 1 orange brown | brown
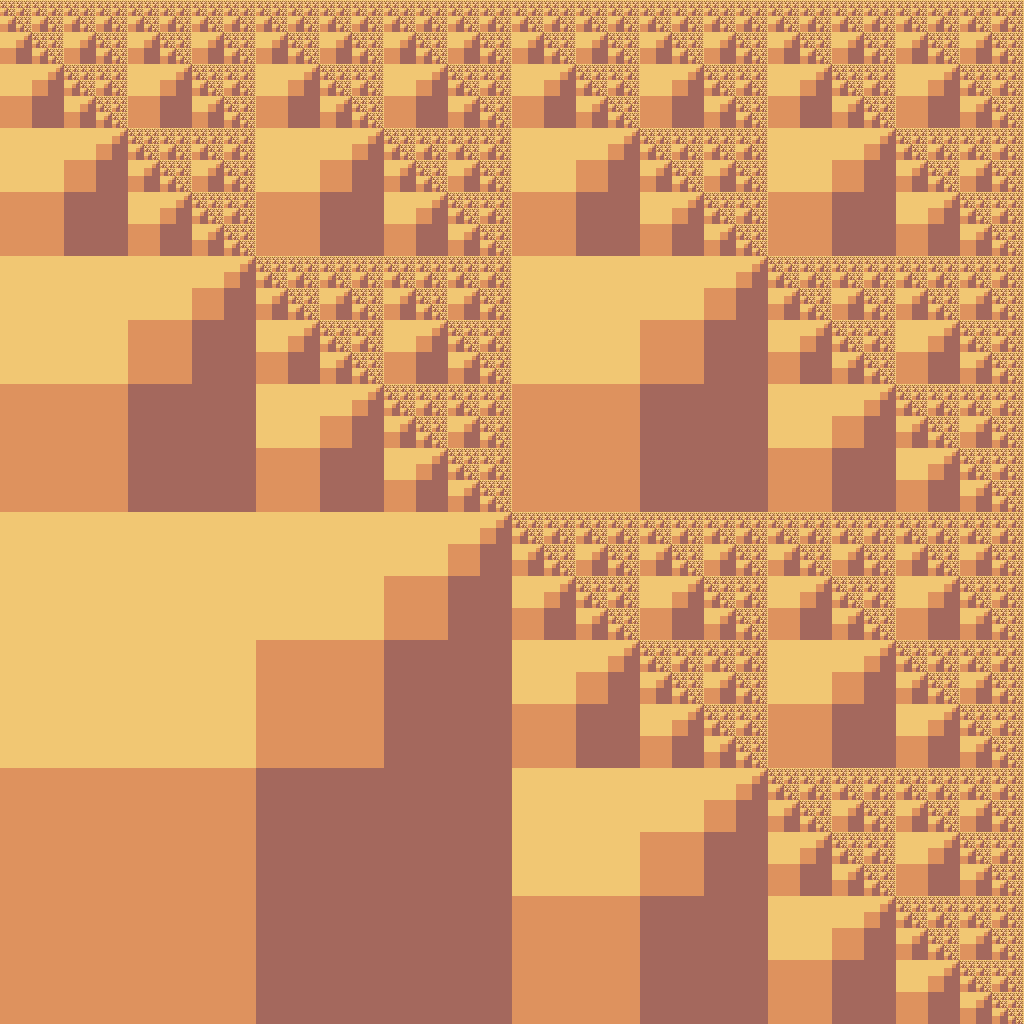
0 -> 1 0 0 0 | yellow 1 -> blue 2 1 1 | blue 2 -> 0 cyan 1 1 | cyan

0 -> 1 3 2 2 | orange 1 -> 1 2 0 brown | brown 2 -> 3 white red 3 | red 3 -> 3 3 1 1 | white

0 -> 1 1 1 1 | cyan 1 -> 0 0 0 1 | white

base16 colors + white, 2 to 4 rules with 1 or 2 branches
0 -> 0 orange 1 0 | orange 1 -> 1 white cyan 1 | cyan

0 -> 0 brown 1 0 | brown 1 -> 0 1 1 yellow | yellow

0 -> 1 2 1 2 | red 0 -> 1 0 orange 2 | orange 1 -> blue brown white 0 | white 1 -> 0 2 0 brown | brown 2 -> 2 1 1 2 | orange 2 -> 1 brown white blue | blue

0 -> 1 0 2 1 | white 1 -> 0 brown 1 1 | brown 2 -> 3 3 1 purple | purple 3 -> 2 3 3 0 | yellow 3 -> 1 0 white green | green
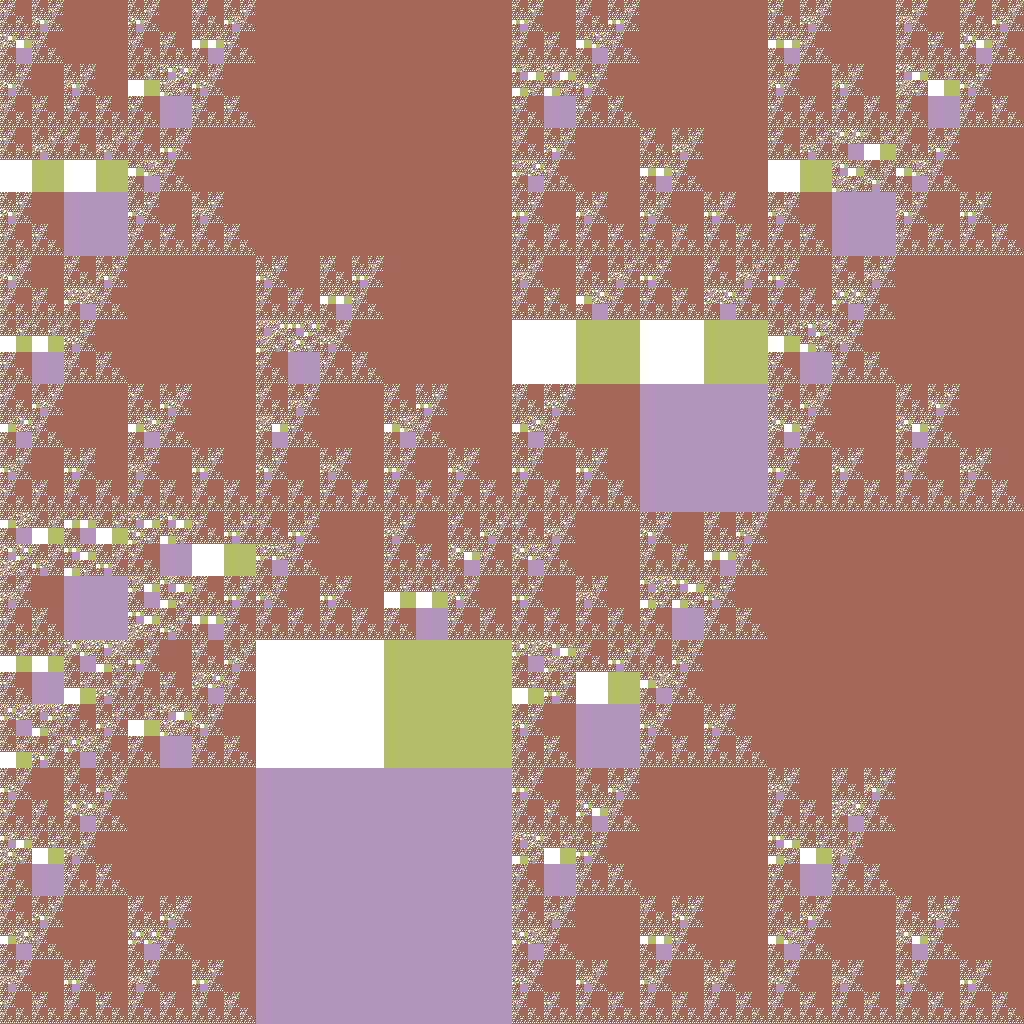
0 -> 0 0 1 0 | white 1 -> 0 1 0 2 | white 1 -> 1 brown 2 0 | brown 2 -> 1 1 cyan 2 | cyan
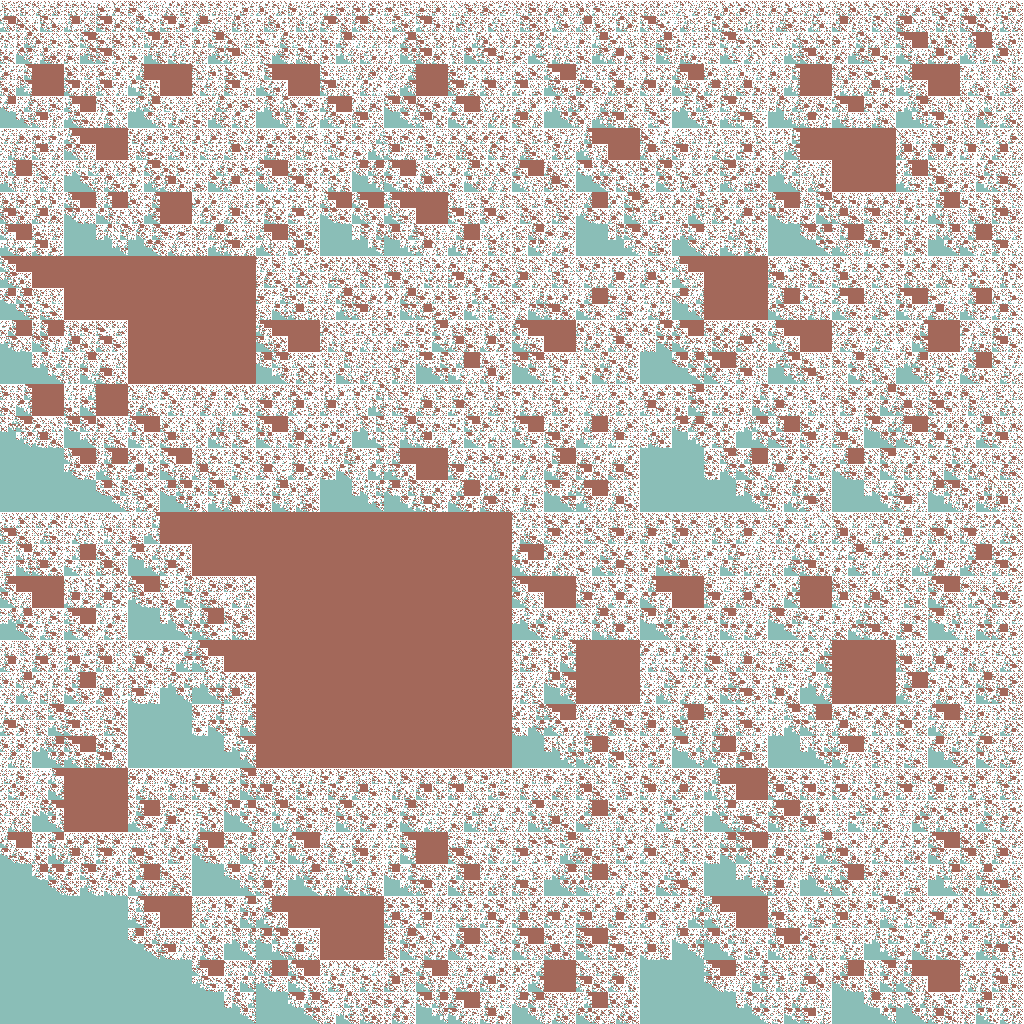
0 -> green 0 1 blue | blue 0 -> 0 yellow 0 1 | yellow 1 -> blue 0 1 purple | purple 1 -> 1 0 yellow 1 | yellow

0 -> 2 0 0 2 | red 0 -> 0 0 blue 2 | blue 1 -> 1 2 1 2 | green 2 -> 1 3 2 2 | orange 3 -> 1 white blue 2 | blue

0 -> 1 1 3 2 | blue 0 -> 0 yellow 3 2 | yellow 1 -> green 1 2 white | white 2 -> red 3 2 3 | red 2 -> blue white 0 2 | white 3 -> blue 3 3 cyan | cyan

0 -> 0 2 2 1 | white 0 -> 2 brown 0 1 | brown 1 -> 1 cyan 0 2 | cyan 2 -> blue 2 cyan yellow | yellow

0 -> 0 1 2 1 | green 1 -> 2 1 0 3 | yellow 1 -> 0 3 3 0 | yellow 2 -> 1 brown white 1 | white 3 -> 2 cyan 3 3 | cyan 3 -> 2 1 1 3 | blue

0 -> yellow 3 1 2 | yellow 1 -> white 3 white 3 | white 1 -> 0 0 3 3 | yellow 2 -> 1 1 3 brown | brown 3 -> 0 1 yellow 1 | yellow
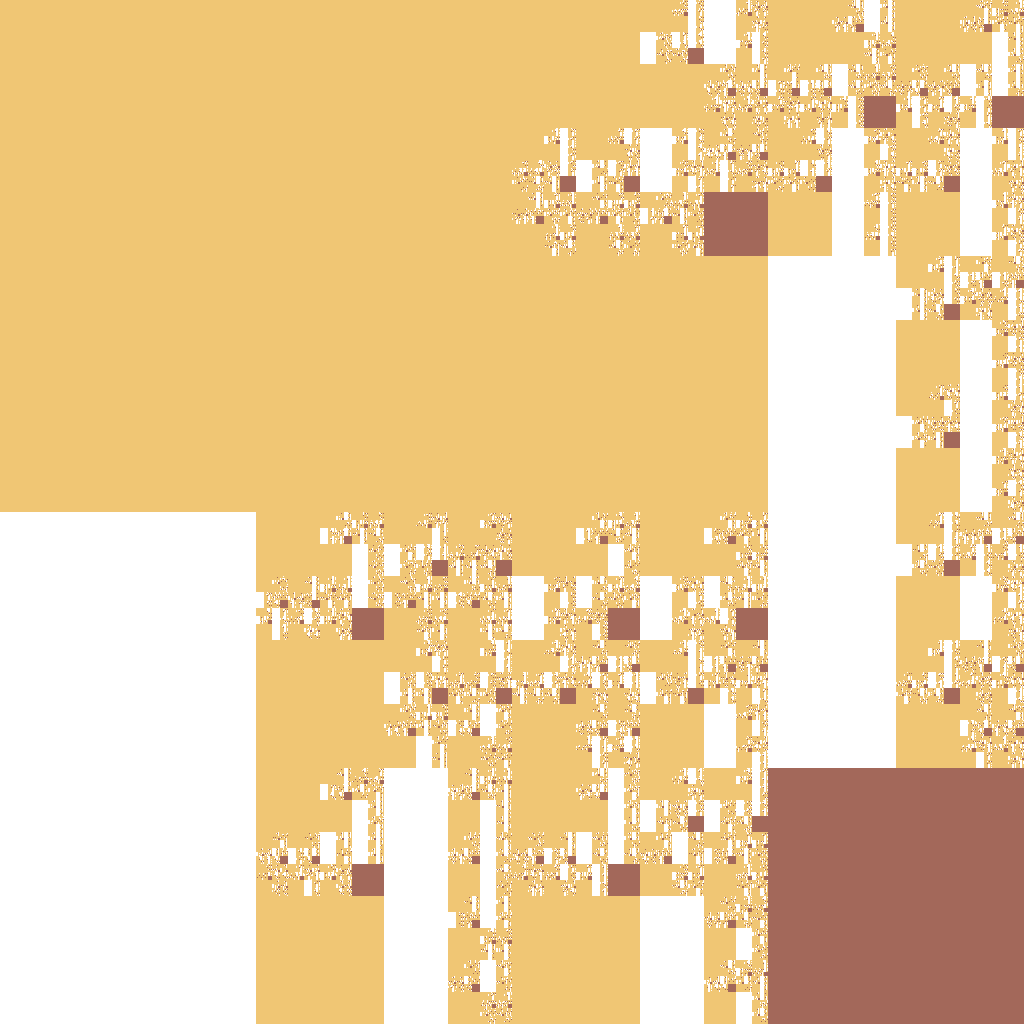
0 -> 0 1 1 0 | blue 1 -> blue 1 white orange | orange 1 -> 0 1 1 yellow | yellow
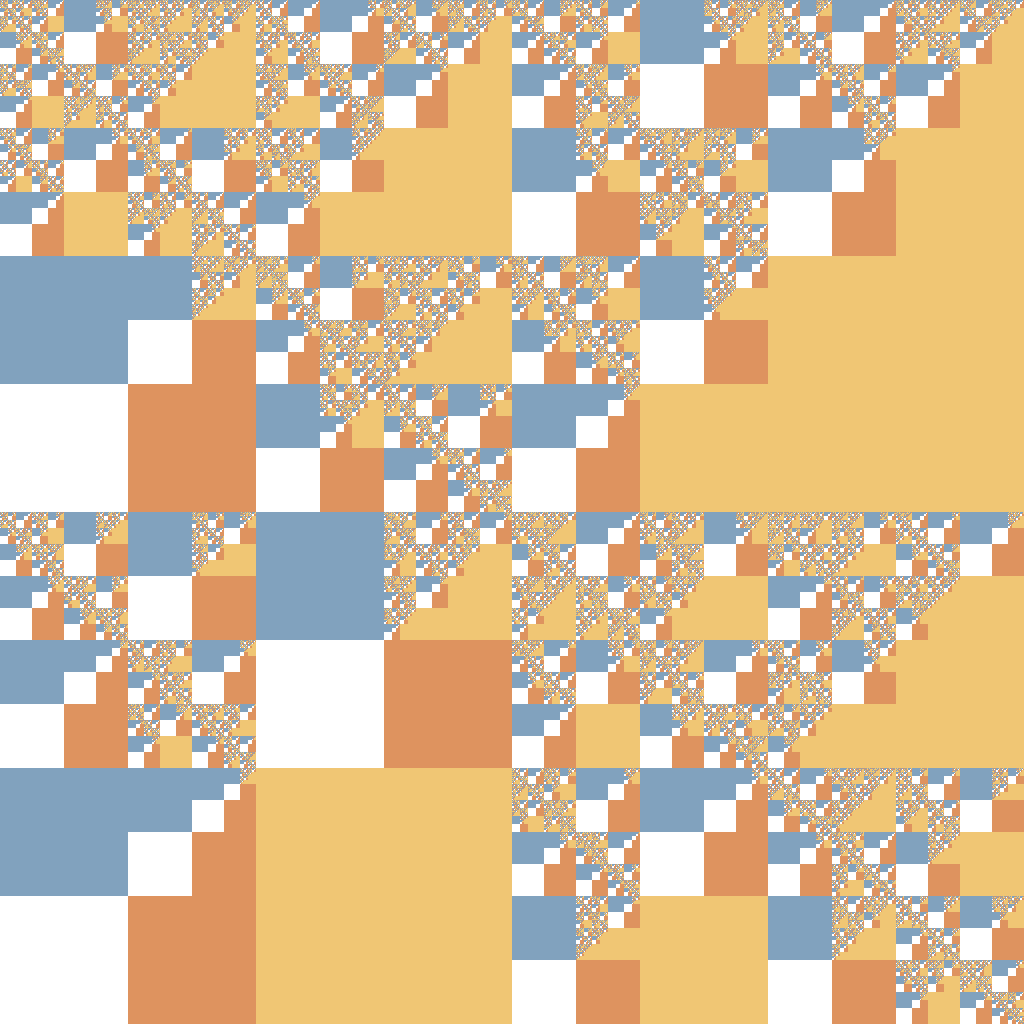
0 -> brown 0 brown blue | blue 0 -> 1 purple 1 red | red 1 -> 0 white red orange | orange 2 -> 0 2 1 2 | orange 2 -> red blue 1 0 | blue

0 -> 0 0 0 1 | red 1 -> 2 1 2 yellow | yellow 2 -> 2 white green 2 | green

Kolmogorov Complexity
We can also think about this in terms of Kolmogorov Complexity , the length of the shortest program that generates a given output.
The size of an (uncompressed) image grows exponentially with regard to the recursion depth, while we just need to pass it as a (e.g. binary, log-size) argument to an implementation of this grammar based generator, in addition to the constant-size rule set.
Under this notion of complexity, we don't care about how many bytes are needed to store the program (or even the operating system it runs on) as their size remains constant and pales in comparison to very large input sizes.
Conclusion
Looking back at my selection from the randomly generated rule sets, the sweet spot seems to be systems with two or three rules, beyond that, the images become to "chaotic".
It should be possible to define a taxonomy of patterns based patterns that show up often, e.g. Sierpinski Triangles, diagonal divisions and recursive binary partitions, but that has to wait for another time.
I'm working on a gallery page with a larger number of images for random rule sets and the source code will be uploaded to github soon.
Another direction to take this would be using simple black and white patterns, shapes and symbols so that the results can be plotted with a pen plotter or using octrees to generate random fractal isometric structures.
References
For the images, I've used colors from the tomorrow-light variant of the base16 color scheme. Thanks Chris Kempson!