Color Quantization with Genetic Algorithms

I removed the images in the post, I hope the code is still useful to someone.

I'm not programming crystal anymore, maybe I'll add a new image at a later time.

For more information on this, see https://www.nature.com/articles/s41565-018-0337-2 .

If you want to follow along, you'll need to install crystal (or rewrite the code in some other language).

We need some way to read and write png images, so run shards init and add following to your shards.yml file:

dependencies:
  stumpy_png:
    github: stumpycr/stumpy_png
    version: ~> 4.2.0

While reading the Handbook of Neuroevolution Through Erlang , I was surprise how simple the description of genetic algorithms (page 87) was:

1. Create a seed population
2. Create a fitness function
3. Loop until termination condition is reached
   1. Evaluate each organism's fitness
   2. Choose the fit organisms from the population
   3. Remove the unfit rest
   4. Create offspring from the fit ones
   5. Compose a new population from the offspring and their parents

Each organism needs a genotype (DNA), a phenotype (how it looks and behaves) and a function that map from one to the other.

I'll use color quantization, representing images with a limited number of colors, as an example. The genotype is a list of colors, the phenotype is how the input image looks after it has been reduced to these colors.

random_color generates a random RGB color (duh) and seed_random creates a palette of size random colors.

require "stumpy_png"
include StumpyPNG

def random_color : RGBA
  RGBA.from_relative(rand, rand, rand, 1.0)
end

class Palette
  def initialize(@colors : Array(RGBA))
  end

  def self.seed_random(size : Int32) : self
    new(Array.new(size) { random_color })
  end

  # ...

quantize maps from genotype to phenotype by finding the color in the palette that is closest to the input color (has the smallest distance ) for each pixel in the image. To save some calculations later, find_closest returns the distance and the closest color. Using the squared distance is faster and because , it won't affect the result.

Note: there are better ways to calculate the distance between two colors, this one is easy to implement good enough for now.

# ...

# Squared euclidian distance between two colors
def distance(a : RGBA, b : RGBA) : Int64
  # Convert to Int64 first, otherwise the subtraction could underflow
  dr = a.r.to_i64 - b.r
  dg = a.g.to_i64 - b.g
  db = a.b.to_i64 - b.b

  dr * dr + dg * dg + db * db
end

def find_closest(input_color : RGBA) : {RGBA, Int64}
  best_color = RGBA::WHITE
  best_distance = Int64::MAX

  @colors.each do |color|
    distance = distance(input_color, color)

    if distance < best_distance
      best_color = color
      best_distance = distance
    end
  end

  {best_color, best_distance}
end

# ...

Now we can build the mapping function, the output / phenotype is a Canvas , a 2D grid of RGBA pixels, with quantized colors. Because find_closest returns a tuple, we need to use [0] to extract the color.

# ...

def quantize(image : Canvas) : Canvas
  Canvas.new(image.width, image.height) do |x, y|
    find_closest(image[x, y])[0]
  end
end

def write(image : Canvas, filename : String)
  StumpyPNG.write(quantize(image), filename)
end

# ...

The fitness function is pretty simple, we just iterate over all pixels of the image and sum up the errors / distances. If one organism is better than another, the value fitness() is smaller .

# ...

def fitness(image : Canvas) : Int64
  image.pixels.reduce(0_i64) { |acc, col| acc + find_closest(col)[1] }
end

# ...

Lastly, we need some way to create offspring for the fittest organisms in our population.

There are various ways to do this:

1. Mutation, copy the genes with a small chance that stuff gets messed up
2. Crossover, combine the genes of multiple parents
3. A combination of both

To keep the implementation as simple as possible, I'll only use the first one.

  # ...

  def produce_offspring(chance) : self
    self.class.new(@colors.map { |color| mutate(color, chance) })
  end

  def mutate(color, chance)
    rand < chance ? random_color : color
  end
end

path points to the image we want to quantize, @population_size tells it how many organisms should be in each generation, @colors is the length of each organism's palette / genes and @mutation_chance can be used to adjust how probable mutations are.

@average_error stores a history of fitness values for the whole population, this is useful to see if the organisms actually improve.

@generations keeps track on how many generations have passed, why this is useful will become clear later.

class Quantizer
  @image : Canvas
  @population : Array(Palette)
  @population_size : Int32
  @colors : Int32
  @mutation_chance : Float64

  def initialize(path, @population_size, @colors, @mutation_chance)
    @image = StumpyPNG.read(path)
    @average_error = [] of Float64
    @population = Array.new(@population_size) { Palette.seed_random(@colors) }
    @generation = 0
  end

  # ...

During each step of the evolutionary loop, we sort the organisms by their fitness, store the average fitness in @average_error for later, take the fittest half of the organisms and create a new population with one offspring each. evolve_to just calls step until the target generation is reached.

write_images iterates over all organisms in the current population and renders their phenotypes, write_average_error creates a .csv file with the average error of each generation.

Math.log10 in combination with .rjust(length, '0') is just a trick to prepend numbers with 0 so that they are all equally long (e.g. =000=…=999= instead of 0 …=999=), this way image viewer display them in the correct order.

  # ...

  def score_fitness
    avg_error = 0.0

    result = @population.sort_by do |palette|
      error = palette.fitness(@image)
      avg_error += error
      error
    end

    n = @population_size * @image.width * @image.height
    @average_error << Math.sqrt(avg_error / n)

    result
  end

  def step
    puts "Generation: #{@generation}"
    new_population = [] of Palette

    fittest = score_fitness[0...(@population_size / 2)]
    fittest.each do |r|
      new_population << r
      new_population << r.produce_offspring(@mutation_chance)
    end

    @population = new_population
    @generation += 1
  end

  def evolve_to(generation)
    while @generation < generation
      step
    end
  end

  def write_images(path)
    Dir.mkdir_p(path) unless File.directory?(path)
    length = Math.log10(@population.size).ceil.to_i

    @population.each_with_index do |palette, i|
      name = path + i.to_s.rjust(length, '0') + ".png"
      palette.write(@image, name)
    end
  end

  def write_average_error(path)
    File.open(path, "w") do |file|
      @average_error.each_with_index do |error, gen|
        file.puts [gen, error].join(",")
      end
    end
  end
end

I'll use a qantizer with a population of 12 organisms, each with 20 colors and a 1% mutation chance as an example.

The input image is Lena, the standard test image .

q = Quantizer.new("./lena.png", 12, 20, 0.01)
q.write_images("images/initial/")

q.evolve_to(10)
q.write_images("images/10/")

q.evolve_to(100)
q.write_images("images/100/")

q.evolve_to(1000)
q.write_images("images/1000/")

q.write_average_error("avg_error.csv")

Initial (random seed population)

In the first (random) generation there already is one pretty good organism, the one at the top right.

After 10 generations it is the dominant version.

Finaly, after 1000 generations and lots of mutations, we arrive at something that looks surprisingly close to the input image.

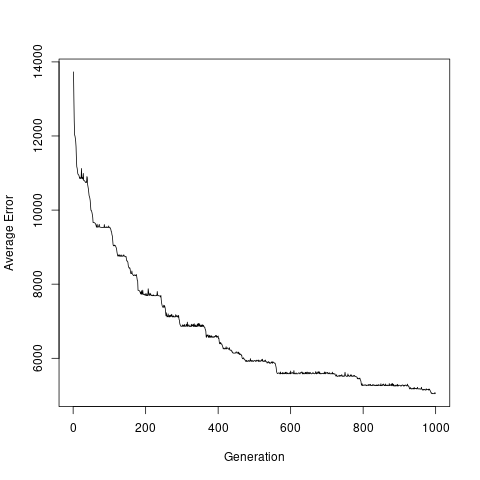
To confirm that the generations get better and better, we can plot the average errors collected along the way:

Images were created using the montage command that ships with ImageMagick .

Full source code: l3kn/genetic_color_quantization .